C阶乘公式是排列组合中的重要工具，用于计算从n个不同元素中选取k（其中0≤ k ≤ n）种元素的特定组合的数目，该公式的应用广泛涉及各个领域如统计学、计算机科学等需要处理数据或分析可能性的场合之中 ，通过运用这一数学原理进行逻辑推理和数据分析 ，人们可以更加精准地解决现实生活中的问题并作出决策判断依据的重要依据之一。。

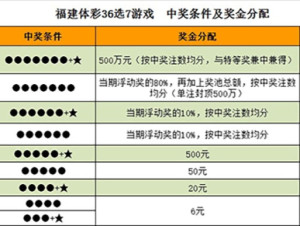
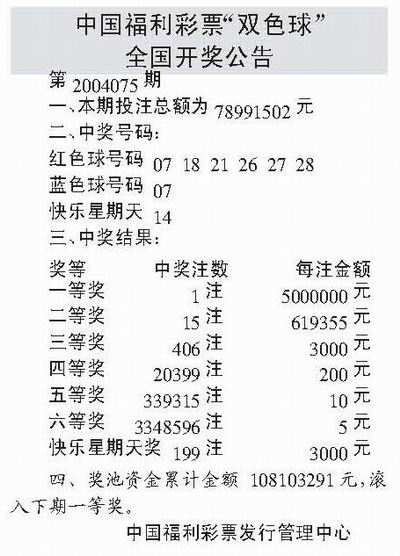
======================= 接下来是正文内容，我们将深入探讨在解决数学问题时，特别是涉及概率和统计的问题时常用的一个关键概念——排 列组合的 C 阶段乘法原则（也被称为选择系数），我们会介绍它的基本概念、使用方法和一些重要的应用实例来帮助读者理解这个概念的重要性以及它在解决实际问题中的应用价值 ，一 、什么是“阶段”或 “层”？当我们谈论到从 n 个不同元素中选取 r个元素的特定情况时，"层次"（Stage）的概念就非常重要了。"分层"意味着我们按照一定的顺序进行选择和操作的过程 ，每个步骤的选择都依赖于前一个步餪的结果。“c 组合数”（Combinations），即我们通常所说的 "n 选 k"，表示的是不考虑排序的从集合中选择多个对象的不同方式的数量在这种情况下，“r 层模型”，或者称为 c 的阶层式计算方式就显得尤为重要了在这种情况下我们可以将问题分解为一系列的子任务每一个这样的任务就是一层每一层的可能性数目相乘就是最终的答案二、“Cn ”的定义及性质首先我们来定义一下这个符号的含义 ：假设有一个包含 N 项的序列其中任意取出 R项的组合数是固定的记作 CR （N ）或者说 CN 表示的就是所有可能的子集的数量在数学上它定义为以下形式："CNR = NN-RR!" "代表当前数的乘积例如如果我们要从一个有五个项目的列表中选出三个项目那么我们的计算公式将是五选三等于五十除以两乘以一的积这就是所谓的 '5Cr' 或更常见的写法为 ''对于任何自然数和正整数来说都有以下的特性存在：（a+b）= a + b；（ab）（ac）＝ ab×bc；这些属性可以帮助我们在处理复杂的数学问题的时候简化运算过程 三、"cn公式的实际应用让我们通过几个具体的例子来看看如何在实际生活中运用这一理论1.彩票抽奖的概率分析以双色球为例这是一种典型的福利彩游戏玩家需要从红蓝两种颜色的号码中各选一个来组成一组中奖规则通常是选中特定的红色数字与蓝色数字的个数越多奖金越高在这个情况下我们就可以利用 cn 理论来计算各种可能的中奖情况比如抽取七个不同的红色的球的方案数为CC(32,7)，而同时再选择一个蓝色的方案的概率为CB因此整个过程的总的可能性就可以表示为两者的结合从而可以计算出某种特殊结果出现的几率从而为购买策略提供依据参考这是该理论的典型应用场景之一当然这只是众多领域中的一个示例实际上这种计算方法在金融风险管理生物信息学计算机科学等领域都有着广泛的应用四总结总的来说了解并熟练掌握基于阶段的计数原理及其相关的数学模型如本文所讨论的关于排列组 合 中的 选择系数的知识对于我们理解和解决实际生活中的许多复杂问题是至关重要的它不仅帮助我们更好地理解随机事件发生的规律也为制定决策提供了科学的依据此外随着大数据时代的到来数据分析和处理的复杂性越来越高掌握这类基础数学知识的能力变得越来越重要在未来的学习和工作中无论是数据分析师还是工程师甚至是科研人员都需要具备扎实的数理基础和强大的数据处理能力以适应日益变化的社会需求以上就是今天对于有关讨论的全部内容和希望这些内容能够帮助大家更好地理解和掌握相关知识在今后的学习实践中不断发展和进步最后感谢大家的阅读和支持期待下一次的讨论和交流！