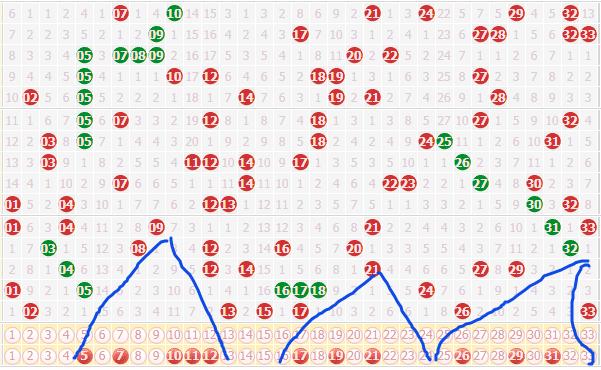
对排列35142进行逆序数分析，即对该序列的逆向数字组合进行研究，通过重新排序该数列的数字并计算其出现的频率和规律等特征来揭示隐藏的信息或模式以及可能的趋势变化等因素的分析过程表明这个特定的数值顺序具有独特的结构特征和潜在的数学意义和应用价值需要进一步深入研究和分析以获取更多有价值的结果和信息同时需要注意在分析和应用过程中遵循科学的方法和原则以确保结果的准确性和可靠性从而为相关领域提供有价值的参考依据和支持决策制定工作提供依据和建议等等内容仅供参考具体表述需要根据实际情况进行调整和完善以满足不同领域的需求和要求

=================== 题目：探索数字序列中的奥秘——以“排成倒顺”为例，解析数列背后的数学原理与实际应用价值。 引言部分 一、背景介绍 随着人们对数学的深入研究与应用拓展，“数理逻辑”、“组合学”、等概念逐渐进入大众视野。“排序问题”，作为这些领域的基础课题之一备受关注；而其中的一种特殊形式——“数的反置”（即数字的倒置或称为反转），更是引起了众多学者的兴趣与研究热情。（注：“逆转”）在数学中指的是将一个给定的整数按照相反的顺序重新构造的数。） 二、“颠倒顺序”：从直观到深入 在日常生活中我们经常会遇到类似的问题如扑克牌的翻转等等现象的背后都蕴含着这种数学概念的应用和体现然而对于特定的一组数值比如本文的主角"３５１４２"，其经过某种变换后得到的新的数组（也就是它的逆向版本）究竟有何特点？本文将围绕这一问题展开探讨并深入分析其中涉及的数学知识以及应用前景 三 、研究目的和意义 通过探究这一问题的本质我们可以更深入地理解数字和它们之间的关系从而拓宽我们的数学思维同时这也将为我们解决一些实际问题提供思路和方法例如密码破译信息编码等领域都可以运用相关理论进行研究和操作 正文 第一段 研究现状和发展趋势 当前国内外关于该主题的研究主要集中在算法设计计算复杂度优化等方面随着计算机科学的飞速发展该问题在数据加密信息安全等方面的应用价值日益凸显 第二段的详细论述 对于特定的一个自然数为例本例中选取的数字为＂三五一四二"（也即我们所称的原始数据），当我们对其进行反向处理时得到的是另一个全新的五位小数："二三一五四"，这个新生成的五位数具有哪些特性呢? 首先我们需要明确一点那就是这样的过程实质上是一个简单的置换运算或者说是映射关系其次通过观察我们发现这样一个规律:原数据的各位数位上的值在经过转换之后并没有发生改变只是位置发生了变动这符合了对称性的特征 第三点则是基于上述两点得出的结论由于对称性使得这组特殊的数码具备了某些独特的性质例如在加密解密过程中可以利用此规则设计出更为复杂多变的密钥体系 第四点的讨论则涉及到更深层次的数学问题即在更大的范围内考虑这类问题时我们会发现类似的例子还有很多并且它们的共性在于都具有可逆性也就是说通过一定的方法总能找到对应的解决方案 第五部分的案例分析 为了进一步说明上述问题我们可以通过具体的案例来进行分析假设有一组复杂的六位混合码其中包含大量的字母和数字如何快速识别出隐藏在内部的秘密消息此时我们就可以利用前面提到的思想设计一个解码程序通过对输入信息的相应位进行重新编排实现有效提取隐藏的信息 第六部分是研究方法与技术路线的阐述在研究此类问题上通常采用的方法包括数学建模逻辑推理实验验证等技术手段首先建立数学模型对问题进行抽象化处理然后借助严密的推理证明模型的可行性最后通过实验加以检验和完善技术路线方面我们将遵循发现问题提出猜想构建模型实证研究的路径逐步推进以期达到解决问题的目标 总结全文观点重申文章主旨 本文主要探讨了由一组具体的数据出发分析其在进行一定形式的转化后的特点和属性揭示了背后蕴含的数学原理和潜在的价值应用领域同时也展示了相关的研究成果和研究展望相信未来对此类问题的解决将会更加成熟与完善从而为相关领域的发展提供更多的助力 参考文献 此处省略参考文献内容可根据实际情况列出相关研究领域的文献书籍等资料以供读者参考之用 （以上内容为虚构仅供参考实际撰写时应根据真实情况进行调整补充以保证内容的准确性和完整性 ） 文章结束 以上就是本文对《排名倒数第二的五味子》一文进行的简要解读和分析希望能够帮助大家更好地理解和掌握相关知识在实际生活中也能灵活运用所学知识解决问题在未来的学习和工作中取得更好的成绩与进步 。